Lattice Math

Lattices are a simple but powerful mathematic concept that can greatly simplify programming distributed systems.

Lattices For Dummies

So, what is a lattice? Lattices are conceptually very simple, so lets explain them without too much mathy language. A lattice is some type of thing that has a very special merge function. The merge function combines two things and produces an output things. The core feature of lattices is that the merge function has some special properties: associativity, commutativity, and idempotence (ACI).

Lets start with a simple example of something which turns out to not be a lattice; numbers and addition. Numbers are a type of thing, and addition is a function that takes two input numbers and produces and output numbers! But does it satisfy the ACI properties?

Let's start with commutativity. A function is commutativity if it doesn't matter if you swap its two inputs: $$a+b=b+a$$ Addition is commutative, so that property is satisfied! (In contrast, subtraction is not commutative).

Next associativity. A function is associative if, when there are multiple calls together, it does not matter in what order you evaluate the calls: $$(a+b)+c=a+(b+c)$$ Addition satisfies associativity! (Again, subtraction is not associative -- if you subtract a subtraction then you're doing addition!)

Finally, idempotence. A function is idempotent if when you give it the same value twice it returns that same value. $$a+a\ne a$$ Addition is NOT idempotent, because $a+a$ is $2a$, not just $a$. This works for $a=0$, but not for all numbers.

Now lets look at something that is a lattice. Numbers and the max function. It is commutiative; the max of $a,b$ is the same as the max of $b,a$. It is associative; the max of $a,b,c$ will always be the same no mater what order you look at them in. And, unlike addition, it is idempotent; the max of $a$ and $a$ is always just $a$.

The most standard, canonical example of a lattice is sets with the union function. It is commutative and associative; it doesn't matter what order you union sets together, the result will always be the same. And it is idempotent; a set unioned with itself is the same set.

Lattice Partial Order

Lattices are tied to and often defined in terms of some sort of "partial order". What is a partial order? It's like a normal order, where you can say "$a$ comes before $b$", but it is partial because sometimes say "$a$ and $b$ are incomparable" instead.

The merge function actually creates a partial order on the elements of the lattice. If you merge $a$ and $b$ together, but the output is still just $b$ unchanged, than we can say that $a$ is smaller than $b$. If you merge $a$ and $b$ and get $a$ out, then $a$ is larger. Finally, if you merge $a$ and $b$ and get a new value $c$ out, then $a$ and $b$ are incomparable.

For the number-max lattice, the partial order created by the max merge function is actually just numerical order. Additionally, it is a total order, meaning all pairs of items are comparable.

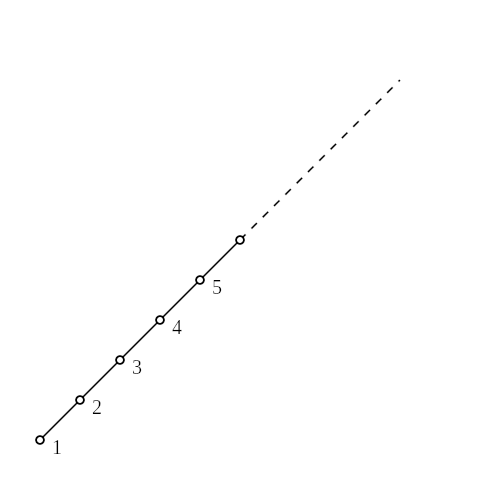A visualization of the max total order over positive integers.

For the set-union lattice the partial order matches subset order. $a$ before $b$ is the same as $a$ is a subset of $b$ ($a\subset b$). If two sets have mismatched elements than they are incomparable.

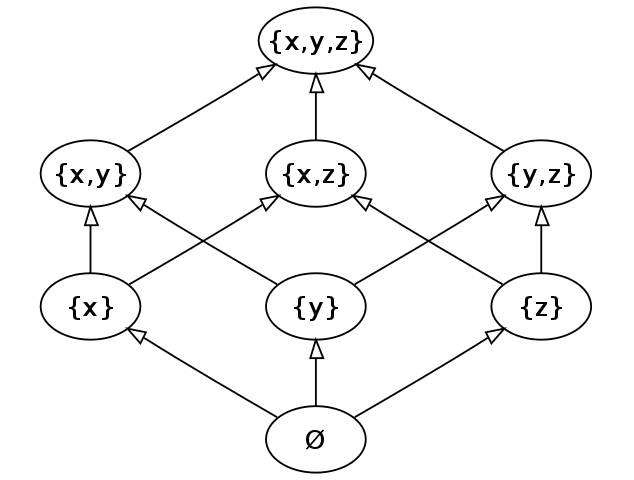A visualization of the set-union partial order over three elements, $x,y,z$. By KSmrq

In the example diagram, $\{x\}$ is less (smaller) than $\{x,y\}$, so there is a path from the former to the later. In contrast, there is no path between $\{x\}$ and $\{z\}$ for example, so they are incomparable.

The merge function is also called the least upper bound (LUB). This name comes from the partial order interpretation. When merging two elements, the result is the smallest (least) item that is still greater than both elements. Hence least upper bound.

Lattice Definitions, At A Glance

A join-semilattice with domain $S$ with $a,b,c\in S$ and join (or "merge") function $\bigsqcup$ has the following properties: $$\begin{gathered} a\bigsqcup (b\bigsqcup c)=(a\bigsqcup b)\bigsqcup c\text{(associative)} \\ a\bigsqcup b=b\bigsqcup a\text{(commutative)} \\ a\bigsqcup a=a\text{(idempotent)} \end{gathered}$$

The join function creates a partial order $⊑$: $$a⊑b\equiv a\bigsqcup b=b$$ Read as "$a$ preceedes $b$", or "$b$ dominates $a$".

The smallest element in a lattice domain $S$, if it exists, is the bottom, $\perp$: $$\forall a\in S,\perp ⊑a$$ The largest element in a lattice domain $S$, if it exists, is the top, $\top$: $$\forall a\in S,\top ⊒a$$

Separately, meet-semilattices and join-semilattices are equivalent structures.

The CALM Theorem and Monotonicity

The CALM Theorem (Consistency As Logical Monotonicity) tells us: "a program has a consistent, coordination-free distributed implementation if and only if it is monotonic"

A function $f:S\to T$ is monotonic if it preserves a partial ordering of its domain to a (possibly different) partial ordering of its codomain. $$a{⊑}_{S}b⟹f(a){⊑}_{T}f(b)\text{(monotonicity)}$$

Lattice Morphism

A function $f:S\to T$ from lattice domain $S$ to lattice codomain $T$ is a morphism if it structurally preserves merges, i.e. merges distribute across the function. For all $a,b\in S$: $$f(a{\bigsqcup }_{S}b)=f(a){\bigsqcup }_{T}f(b)\text{(morphism)}$$ (Because both the domain and codomain are semilattice spaces, semilattice homomorphism is the most precise term for this.)

Lattice morphisms are a special kind of monotonic function which are differentially computable. Because merge distributes over a morphism, we can evaluate the morphisms on a small "delta" of data and merge that delta into the existing result rather than recompute the entire morphism on all data.

Further Reading

• The Hydroflow Thesis